Exploration Through Example

Mark Needham asked on twitter:

I replied:

He replied:

Since I’m in an explaining sort of mood this week, let me see if I can help.

Suppose I’m working with some sort of tree. This image comes to mind:

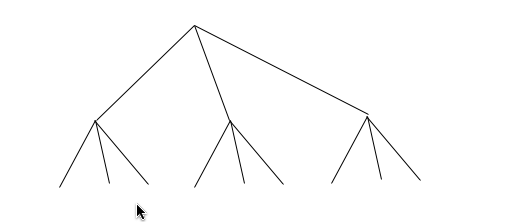
What I see is a big tree with three little trees under it. I can easily see how to split it up into little trees:

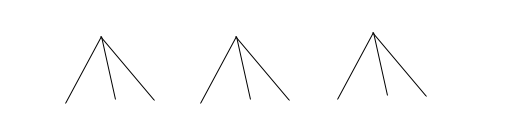
Because the big tree is composed of little trees, the Big Answer must be composed of little answers. This lets me know that I need to answer three questions:

1. How do I split up the big tree? That’s probably pretty easy—for example, iterating down an array.

2. How do I ask the little trees for the little answers? With luck, that’s exactly the same as asking the big tree for the Big Answer. Even without luck, it’s probably almost the same.

3. How do I compose little answers into the Big Answer? That’s often the harder part. Mostly, there are various tricks of the trade you just need to learn and remember.

Now, if you continue splitting up the big tree, you run into this:

These don’t look like little trees any more. They’re something different—leaves. That means there are two more questions I need to ask:

4. How do I tell the difference between a tree and a leaf?

5. How do I get the tiniest answer from a leaf?

So, for example, if I had a tree of values like this:

[    [   [1 2 3]   3   [1 2] ] 3 ]

… and I wanted to add up all the values, I could approach the problem like this:

1. I can split up the tree by iterating over a list. So I know I’m going to do something like this (in Ruby):

     def sum(tree)
      tree.each { ... }  # or
      tree.collect { ... } # or
      tree.reduce(...) { ... }
   

2. I can ask the subtrees for their values with the method I’m in the middle of defining. That suggests something like this:

     def sum(tree)
      tree.collect { | subtree | ... sum(subtree) ...}
   

3. How do I compose the answers? One way is to use a library method called `reduce`—but if recursion is confusing, `reduce` probably doesn’t help. So let me backtrack and use a common idiom, the collecting parameter. I’ll pass the “sum so far” around, and have subtrees adding to it.

That means revising my earlier answers…

1. I still break up the list by iterating over it.

2. I ask the subtrees to add their value to the sum-so-far:

     def sum(tree, sum_so_far = 0)
       tree.each { | subtree | sum_so_far = sum(subtree, sum_so_far) }
       ...
   

How do I compose the answers? Well, I no longer have to. The last `sum_so_far` is the answer.

  def sum(tree, sum_so_far = 0)
    tree.each { | subtree | sum_so_far = sum(subtree, sum_so_far) }
    sum_so_far

3. I can tell if I’m at a leaf by asking the “subtree” if it’s Numeric:

     def sum(tree, sum_so_far = 0)
       tree.each do | subtree |
         if subtree.is_a?(Numeric)
           ...
         else
           sum_so_far = sum(subtree, sum_so_far)
         end
       end
       sum_so_far
     end
   

4. Getting the value “out” of the leaf is just a matter of adding it to the `sum_so_far`:

     def sum(tree, sum_so_far = 0)
       tree.each do | subtree |
         if subtree.is_a?(Numeric)
           sum_so_far += subtree
         else
           sum_so_far = sum(subtree, sum_so_far)
         end
       end
       sum_so_far
     end
   

This isn’t a great solution, but it works. It’s also somewhat artificial, in that I walked through the questions in order. In real life, some of the questions are more incisive for a particular problem than others, so asking them first would be better than waiting until they come up in the list. (And I hardly ever think about the questions so explicitly, but that’s the usual conversion of explicit into tacit knowledge.)

Reduce

I mentioned that the `reduce` method seems to confuse people. If the above code is clear, it might help to think of `reduce` as just a simplification of it. Reduce is always working with a “so far” argument that it keeps adding to, a collection it maps over (as with `each`), and individual elements of the collection that get added (somehow) to the so-far argument. So the equivalent of the above code would be this:

  def sum(tree)
    tree.reduce(0) do | sum_so_far, subtree |
      if subtree.is_a?(Numeric)
        sum_so_far + subtree
      else
        sum_so_far + sum(subtree)
      end
    end
  end

This code does the same thing; we just didn’t have to write out as much manipulation of `sum_so_far`. We don’t have to assign a new value to it, because `reduce` does it (or what amounts to assignment) for us, and we don’t need to explicitly return the `sum_so_far` because that’s what `reduce` returns.

Flatten

Another way to implement recursion is to let someone else do the work for you. In this particular case, the final answer doesn’t depend on the shape of the tree. That is, these two trees have the same Big Answer:

[    [   [1 2 3]   3   [1 2] ] 3 ]
[         1 2 3    3    1 2    3 ]

So we don’t have to intertwingle addition and traversing the tree. We can do them separately. That’s particularly nice because we already have a method that traverses a tree and gives you just its leaf nodes: `flatten`. So my final version of the program is this:

  def sum(tree)
    tree.flatten.reduce(0) { | sum_so_far, n |
      sum_so_far + n
    }
  end

Testing

If the answers to any of the questions seem at all difficult, I make them into separate methods and test-drive them. Then I test the whole thing on data that is just the base case (there’s nothing but a leaf) and also on a nested case. Plus whatever other tests the structure of the data suggests.

An alternative would be to build up the algorithm by making `sum` work with only the base case, then adding on. I don’t do that, at least not for simple data (nothing but one kind of leaf and one kind of tree).